Electric Fields
Electric fields are generated by two means:
- Static Charge
-
Time varying
- A charge at rest generates an electric force field $\underline{E}$
-
Around this point as the distances increases electric field decreases
- If the $\underline{E}$ field generated by a single point is know then it’s charge distribution can be calculated, this can be done by the vector sums of the $\underline{E}$ fields each postition of charge.
Coulomb’s Law
The magnitude of $\underline{E}$ at the radial distance $r$ from a point charge $q$ in free space is propotional to the size of charge $q$ and inversely proportional the distance $r$.
\[E=\frac{q}{4 \pi \epsilon_0 r^2}=k\frac{q}{r^2}\]This is an example of an inverse square law field, $\epsilon_0 = 8.85 \times 10^{-12} (F/m)$ $k=(4 \pi \epsilon_0 r^2)^{-1}=8.99 \times 10^9 (m/F)$
Direction of E Field
If charge:
- $+$ source / Point away from the charged particle
- $-$ sink / Point towards from the charged particle
Electric Potential
- Electric potential $\phi$ is a scalar quantity of S.I. unit volt, V.
- Every point in space has a unique/single value of $\phi$
- $\phi$ is increased at a point (made more positive) by bringing more positive charges nearby
- If $\phi$ varies in some region $E > 0$ but if it is constant then $E=0$
In 1-D electric potential are linked by the negative of the graident of the slope (- the poteintial gradient), more generally $\underline{E}=-\nabla \phi$
Electric Potential Energy
- EPE is used to link Electric Potential to work and energy
- The EPE of a charge $q$ placed at position A is calcualted by the expression $U_A = q \phi_{A}$
The work done on moving a charge between any two points depends on their difference in electric potentials, not the path taken.
- The potenital diffrence between two points is called the $Voltage$ $V_{BA} = = \phi_{B} - \phi{A} = \frac{W_{BA}}{q}$
The work done on moving a charge between any two points depends on the difference between their electric potentials not their path taken
The poteintial difference between the two paths are point $A$ and $B$ is called a voltage $V_{BA}=\phi_{B} - \phi_{A} = W_{BA}/q$
Note $V_{AB} = -V_{BA} \therefore W_{AB}=-W_{BA}$
Defining Equations
\[\underline{F} = q\underline{E}\] \[W_{BA}=q(\phi_{B} - \phi_{A})= qV_{BA}\] \[\underline{E}=-\underline{\nabla}\phi\]The electric potential of a uniform E field
- This type of Electric fields are setup between two chraged metal sheets of spacing (eg parrallel plate capacitor) constant $E$ means $\phi$ varies linearly with distance
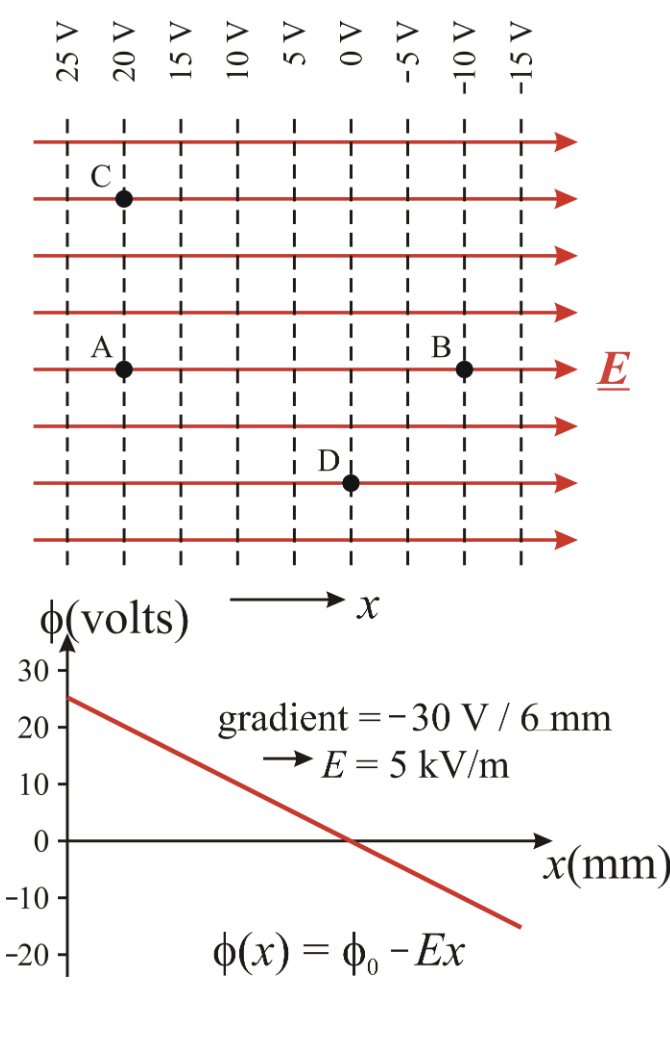
The ‘dotted’ lines are actually surfaces (parallel planes) - equipotential surfaces on which $\phi$ is constatnt everywhere
- The electric field always points in direction of decreasing $\phi$
- The electric field is alway perpindicular to the direction of the equipotentials
- E is largest where all the equipots buch up
For unifrom electric field the equipotentials surfaces are equally spaced planes
- The potential gradient is the space between two points will be in the form $Voltage/distace$
$y=mx +c \ \phi(x)=\texttt{Crossing Y Interncept} + \texttt{Gradient}(x)$
Electric potential and equipotentials of a point charge
The potential difference between a point at a distance $R$ from the charge can be found:
\[\phi(R) = \frac{q}{4 \pi \epsilon_{0} R}\]$+$ charge rasies the electric potential whereas negative charge lower’s it